Segment Tree

Introduction

Segment tree is used to efficiently answer dynamic range queries, which is abbreviated as a RMQ problem. Suppose there is an array of size $n$. The question is to find the index of the minimum element in an array with range $[i, j]$.

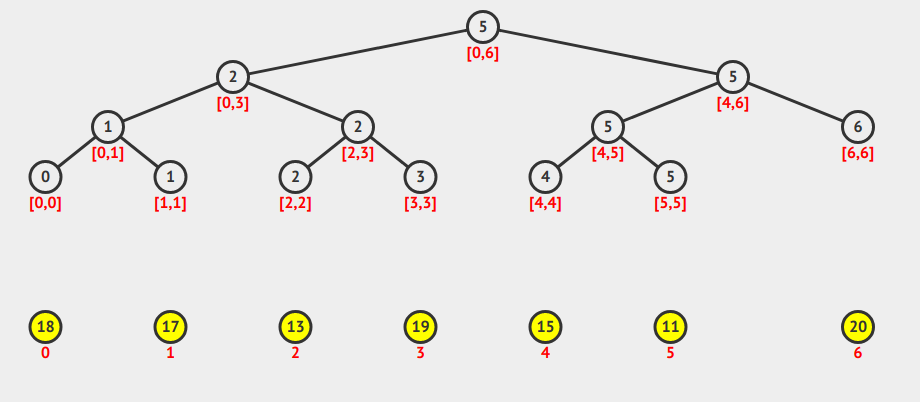
For example if we have the following data in an array $A$:

Index	0	1	2	3	4	5	6
Value	18	17	13	19	15	11	20

Then, $RMQ(0, 6) = 5$, $RMQ(0,4) = 2$.

The brute force solution is to traverse every element between the two given indices, which will take $O(n)$ time per query. To improve it, Segment tree can be used which takes $O(n)$ time to construct and $O(\log n)$ time per-query.

Segment tree is a binary structure in theory. But for simplicity, we are going to use 1-based compact array to represent it. In implementation, this will be vector<int> st. Under such settings, index 1 (skipping index 0) is the root and the left and right children of index $p$ are at index $2p$ and $2p+1$ respectively. The value of sp[t] is the RMQ value of the segment associate with index $p$.

The root of segment tree represents segment $[0, n-1]$. For each $[L, R]$ stored in index $p$ where $L!=R$, the segment will split into $[L, (L+R)/2]$ and $[(L+R)/2 + 1, R]$ in a left and right vertices. This building process runs recursively until leaf nodes are hit where $L=R$.

Answering for $RMQ(i, j)$ query where $i < j$ is done recursively. Let $p1 = RMQ(i, (i+j)/2)$ and $p2 = RMQ((i+j)/2 + 1, j)$. Then compare $A[p1]$ with $A[p2]$, set the answer to be the smaller one. Detailed implementation is showed below.

Segment Tree (VisuAlgo)

When to Use Segment Tree

Note that segment tree is overkill for static range queries. There exists $O(n \log n)$ Dynamic Programming solution for it which takes only $O(1)$ time per-query. The idea is to build a table where $i, j$ position value is the minimum value for the sub-array starting at position $i$ with length $2^j$. I will try to describe the details in another post. However, when the original array is frequently updated, segment tree is very useful and efficient.

Implementation

Header File

The following is segment_tree.hpp file.

#ifndef MY_SEGMENT_TREE
#define MY_SEGMENT_TREE
#include <vector>
#include <iostream>

class SegmentTree{
private:
  // st is 1-based conpact array
  // A is the original array
  std::vector<int> st, A;
  // n is the size of the data array
  int n;
  // get left child index in compact array
  int left(int p){ return p << 1; }
  // right child index
  int right(int p) { return (p << 1) + 1; }

  // function to build segment tree
  void build(int p, int L, int R){
    if(L == R) st[p] = L;
    else{
      // recursively compute the values
      build(left(p) , L            , (L+R) / 2);
      build(right(p), (L+R) / 2 + 1, R        );
      int p1 = st[left(p)], p2 = st[right(p)];
      st[p] = (A[p1] <= A[p2]) ? p1 : p2;
    }
  }

  // recursive function for doing query
  int rmq(int p, int L, int R, int i, int j){
    if (i > R || j < L) return -1; // outside of the range represented by st[p]
    if (i <= L && j >= R) return st[p]; // within the query range, than st[p] is needed

    // compute the min position in the left and right
    int p1 = rmq(left(p) , L            , (L+R) / 2, i, j);
    int p2 = rmq(right(p), (L+R) / 2 + 1, R        , i, j);
    if (p1 == -1) return p2;
    if (p2 == -1) return p1;
    return (A[p1] <= A[p2]) ? p1 : p2;
  }

public:
  SegmentTree(const std::vector<int> &_A){
    A = _A; // copy content from local usage
    n = (int)A.size(); // set size for data array
    st.assign(4*n, 0); // assign enough number of zeros
    build(1, 0, n-1); // use index 1 in st as root, build ST
  }

  int rmq(int i, int j){ return rmq(1, 0, n-1, i, j); } // overloading, start searching from root
};

#endif

Test File

Test it with the following code (main.cpp):

#include <iostream>
#include "./include/segment_tree.hpp"

int main(){
  int arr[] = {18, 17, 13, 19, 15, 11, 20};
  std::vector<int> A(arr, arr + 7);
  SegmentTree st(A);
  std::cout << "RMQ(1, 3) = " << st.rmq(1, 3) << std::endl;
  std::cout << "RMQ(4,6) = " << st.rmq(4, 6) << std::endl;
}