Pregel PageRank: A Simple Java Implementation

Introduction

This is a project I am doing for a course. The project’s goal is to simulate computing PageRank in a Pregel like system with multithreading in Java.

Some Basic Information

Pregel: A System for Large-Scale Graph Processing

Pregel Paper

PageRank

PageRank Original Paper, and PageRank Wikipedia

Message Queue

Message Passing with Threads & Queues

Review for Java Threads

Java Threads

Important Details about Pregel

Vertex

• compute() woule be executed at each active vertex in every superstep.
• compute() is allowed to query information about the current vertex and its edges and to send messages to other vertices.
• compute() can inspect and modify the values of out-edges using methods supplied by the out-edge iterator.
• The values associated with the vertex and its edges are the only pre-vertex state that persists across supersteps.

Message Passing

• Vertices communicate directly with one another by sending messages.
• A message consists of a message value and the name of the destination vertex.
• Messages sent to vertex $V$ in superstep $S$ are available via an iterator, at superstep $S+1$.
• There is no guarantee on order of messages in the iterator, but it is guaranteed that messages will be delivered and that they will not be duplicated.

Aggregators

• Each vertex can provide a value to an aggregator in superstep $S$, the system combines those values using a reduction operator.
• Resulting value is made available to all vertices in superstep $S+1$.
• Define a new aggregator by creating a subclass of Aggregator, which is a predefined class. And specify how the aggregated value is initialized from the first input value and how multiple partially aggregated values are reduced to one.

In PageRank task, I am considering using Aggregator’s subclass instance(maybe a function is enough for this project) to aggregate message values sent to the same vertex.

Worker Implementation

• The state of each vertex contains:
  • current value
  • a list of outgoing edges
  • a queue containing incoming messages
  • a flag specifying whether the vertex is active

When the worker performs a superstep it loops through all vertices and calls compute(), passing it the current value, an iterator to the incoming messages, and an iterator to the outgoing edges.

• Two copies of the active vertex flags and the incoming message queue exist: one for the current superstep and one for the next superstep

Master Implementation

Primarily, the master is responsible for coordinating the activities of workers. Most master operations, including input, output, computation, and saving and resuming from checkpoints, are terminated at barriers.

Aggregator Implementation

An aggregator computes a single global value by applying an aggregation function to a set of values that the user supplies. When a worker executes a superstep for any partition of the graph, the worker combines all of the values supplied to an aggregator instance into a single value.

My Thoughts

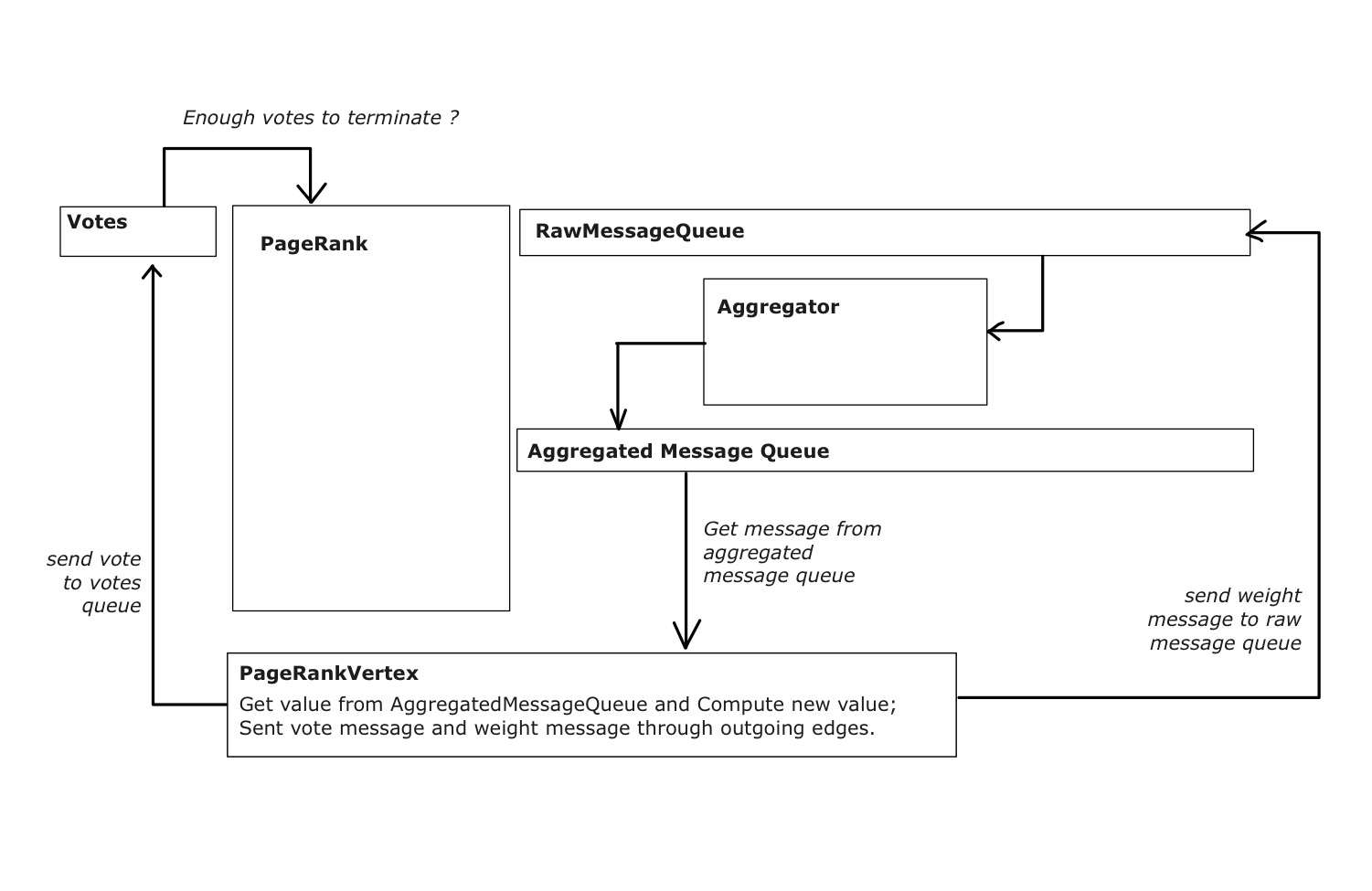
Structures

PageRank Class

• Initialize edges; create vertices; set superstep to zero
• Start all vertices’ threads
• While number of vertices that voting to halt is smaller than size
  • clear votes; clear rawMessageQueue; clear AggregatedMessageQueue
  • superstep += 1
  • Send message to all vertices for starting next superstep
  • while voteCount is smaller than size
    • Count votes received and add it to voteCount
  • Aggregate rawMessageQueue into AggregatedMessageQueue
  • Count number of -1 in votes

Vertices

• Up on start, halt
• waiting for a message from Master that indicates starting of next superstep
• get the aggregated message from the in-message-queue.
• Tallcompute(), where the new weight, messages' value,error, vote message would be computed or generated.
• Pause thread and wait for next superstep to start

Message Class

Class Message is used for holding message information. It has several attributes:

• type: Int
• from: Integer
• to: Integer
• value: Double
• isVote: boolean
• vote: Int

where, type indicates that if this message is a vote or a message that passing weight; from, to marks the sender and receiver of this message; value holds the weight, would be null if message is a vote; isVote is a flag for marking votes message; vote indicates whether the vertex is voting to halt or not.

Compute() function

• Calculate new weight:

$$R = \frac{0.15}{n}+0.85 \sum_{j\in N_{in(i)}} M[j]$$

• Calculate message value:

$$M = \frac{R}{\left|N_{out}\right|}$$

• Send $M$ to all its outgoing edges’ destination
• Calculate error:

$$error = R - R_{previous}$$

• Vote to halt (1 for voting to halt, -1 otherwise)
• Wait on superstep

Note that initially, every vertex’s weight would be set to $\frac{1}{\#vertices}$. Also, in the very first superstep, the error shouldn’t be computed because there are no $R_{previous}$ value available.